I have an assignment that involves building a language identifier (given text, predict which language is the text from) using Neural Nets. I wanted to use this opportunity to make a few posts to cement the idea into my head. I hope you find this intuitive and helpful.
So lets talk about NN in terms of classification, when I think of neural networks, I think of applying a multi-layered system to make a decision. Your feed the NN your data or information, it is then linearly transformed, then a nonlinear function is used on the linear transformation to further transform the information. Another linear transformation is done on the output of the non-linear function, then yet another nonlinear function (it can be different from the first) is used, so on and so forth. At the end of these transformations, a decision/classfication is made. One question I asked is why apply this linear then nonlinear transformation. To answer this, lets look at the units that make up NN and then at decision boundaries and how linear ones fail the XOR problem.
Units
This part will be brief. Just think of a unit as a weighted sum of the inputed data, plus an additional bias term. This looks like the following: \(\sum_{i=1}^{n}{w_{i}x_{i}} + bias\) where \(w_{i}\) are weights that correspond to each value in the data.
The XOR problem
The XOR problem takes two binary inputs, x1 and x2, and if x1=x2, then the result is classified as 0. If x1 != x2, then it is classified as 1. This is why the X in XOR stands for “exclusive”. So if we plot the combinations of x1 and x2, we get the plot below. If the point is red, then the x1, x2 combo was classified as 0. Similarly, blue points are classified as 1. 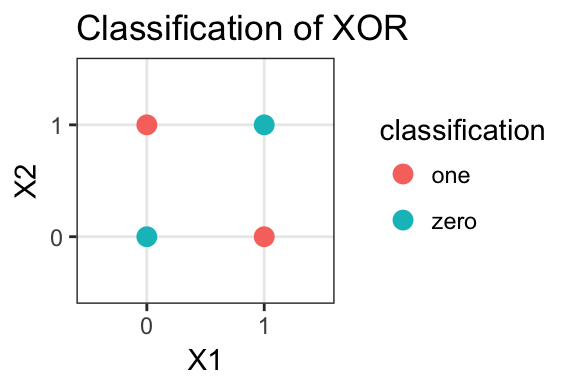 Now, there are similar problem like XOR, known as AND. The solution to give the correct classification of is \(y = 1\) if \(\sum{w_{i}x_{i}} + b > 0\). Else, \(y=0\). To show that the formula works, take \(w_{1} = w_{2} = 1\) and \(b = -1\). Then \(\sum{w_{i}x_{i}} + b > 0\) if and only if \(x_{1} = x_{2} = 1\). Now, observe that the plot of the AND problem looks like this.
Now, there are similar problem like XOR, known as AND. The solution to give the correct classification of is \(y = 1\) if \(\sum{w_{i}x_{i}} + b > 0\). Else, \(y=0\). To show that the formula works, take \(w_{1} = w_{2} = 1\) and \(b = -1\). Then \(\sum{w_{i}x_{i}} + b > 0\) if and only if \(x_{1} = x_{2} = 1\). Now, observe that the plot of the AND problem looks like this. 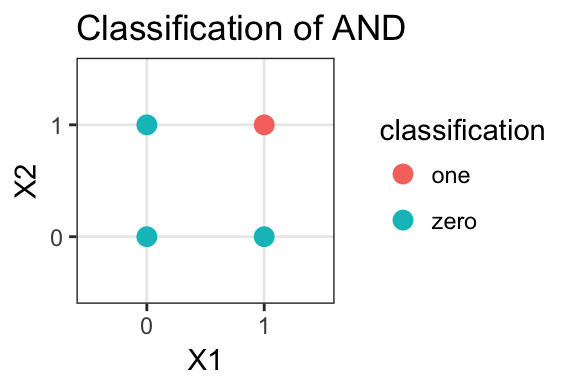 Now what’s the key difference between the two plots? For the second plot, you can draw a straight line to separate the red point from the others. You can’t do this for the first plot. This is because the AND problem has what is known as a linear decision boundary. Another way of viewing this is is that \(\sum{w_{i}x_{i}} + b = 0\) is the equation of a line. All points to the right of the line would be points such that the sum is greater than 0, and thus would be classified as ‘One’. For the points on the left of the line, they are classified as ‘Zero’. This equation of a line is then the boundary of which decision to make. Since it’s a linear function, it’s called a linear decision boundary. Since the XOR problem can’t be separated by a straight line, it’s known as a not linearly separatable.
Now what’s the key difference between the two plots? For the second plot, you can draw a straight line to separate the red point from the others. You can’t do this for the first plot. This is because the AND problem has what is known as a linear decision boundary. Another way of viewing this is is that \(\sum{w_{i}x_{i}} + b = 0\) is the equation of a line. All points to the right of the line would be points such that the sum is greater than 0, and thus would be classified as ‘One’. For the points on the left of the line, they are classified as ‘Zero’. This equation of a line is then the boundary of which decision to make. Since it’s a linear function, it’s called a linear decision boundary. Since the XOR problem can’t be separated by a straight line, it’s known as a not linearly separatable.